Calculation of Pressure Loss in Corrugated Hoses

When designing piping systems, it’s important to consider pressure loss, or drop, through the hose. This will allow you to assess its impact on the piping system’s operation.

It’s a difficult calculation—being based on flow rate (volume per time)—and one that depends on several variables including the type of media passing through the hose, the geometry of the hose and the application setup. The only way to truly determine pressure drop in a hose is to set a gauge at one end and another at the other, and to then take a reading.

However, if accurate readings of inlet and outlet pressure are not readily available, we can roughly estimate pressure drop in a corrugated hose based on what we would see in steel pipe under similar flow conditions. Due to its profile, pressure loss in corrugated hose is significantly higher than that in steel pipes. As a general rule, pressure drop in the turbulence zone of corrugated hose will be 150% higher than in steel pipe while pressure drop in the high velocity zone will be 450% higher.

Pressure Loss Scenario

For example, let’s say we need to calculate the pressure loss in 2” (ID) corrugated hoses that are 85 feet long and transferring water with flow rate of 1400 cubic feet per hour.

By using Penflex’s Pressure Loss calculator we find that 1400 ft³/hour corresponds to 175 gal/min.

To convert flow rate from Cubic Feet per Hour to Gallons per Minute, use the calculator below:

Then we plot the 175 gal/min on the X-axis of this chart until we “hit” the line for 2″ hose ID, then by going over horizontally to the Y-axis, we find that pressure loss per foot of hose will be about 3.7 psi.

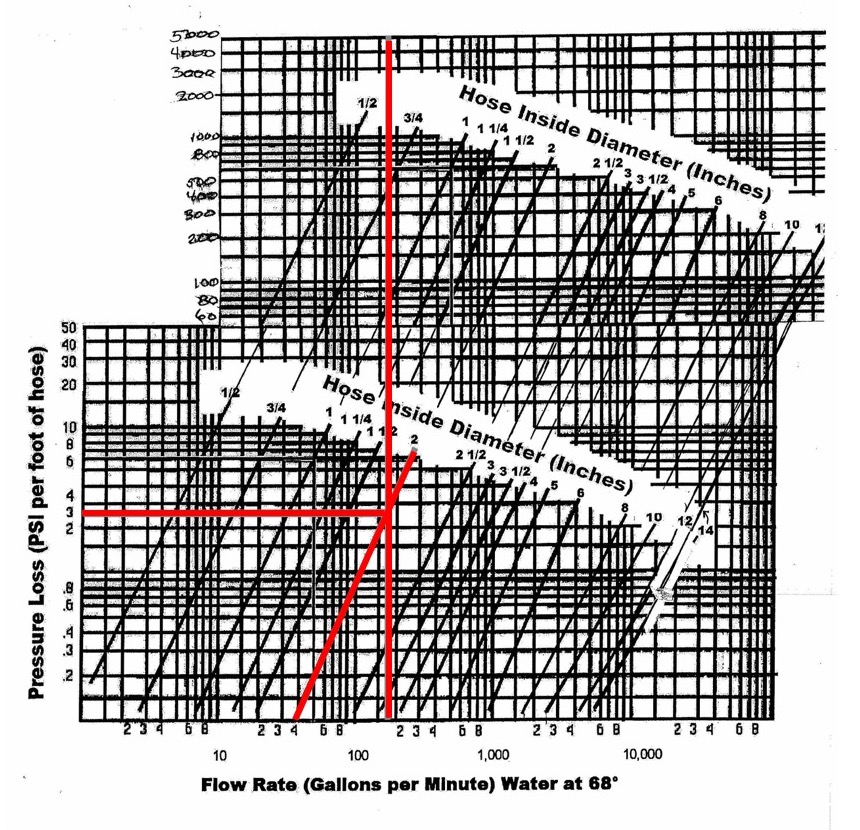
Thus, the total pressure drop over the hose length will be 314.5 psi (3.7 psi x 85 feet).

Keep in mind that if you transfer gaseous substance through the hose then you need to find the ratio of the density of gas over the density of water and adjust the pressure drop respectively.

For example if you transfer natural gas (density = 0.050 lb/ft3) and knowing that water density is 62.4 lb/ft3 we can find out the pressure drop as the following: 3.7 psi x (0.050/62.4) = 0.0030 psi/ft or 0.255 psi for entire length of hose (85 x 0.003).

For calculations relevant to your application, you can download and print a blank chart.

Please contact us with any questions.